Adapting Learning Rates in Full Precision Training to Half Precision Training on TPUs
Upshot
When training in bfloat16 small gradients may get nullified due to rounding. In particular, this may prevent model parameters from evolving at all. Sophisticated approaches to avoid this problem, including introducing stochastic rounding and gradient accumulation techniques have been detailed in the literature, but one very simple way to handle this issue is to simply scale the learning rate and batch size simultaneously until training proceeds properly.
Acknowledgements
My access to TPUs is graciously provided by the TPU Research Cloud ! This blog post and my research efforts would not be possible without their support !
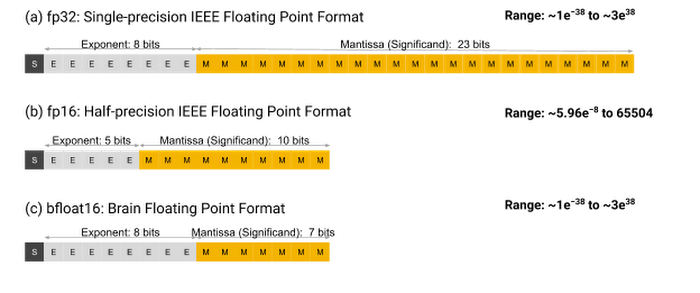
bfloat16 vs float32
Float32 is a 32 bit floating point format that consists of 1 bit to specify the sign, 8 bits to specify the exponent, and 23 bits to specify the mantissa.
Image taken from BFloat16: The secret to high performance on Cloud TPUs
The mantissa bits control with how much precision any given rational number between two exponents can be expressed. More mantissa bits equate to more precision. As the exponent increases, the fixed amount of expression provided by the mantissa bits decreases sharply as the same number of bits must be used to describe an exponentially larger range of rational numbers.
This lack of precision at larger rational numbers is the cause of training difficulties when using bfloat16. As a brief introduction to bfloat16 - bfloat16 is a 16 bit floating point format consisting of 1 sign bit, 8 exponent bits, and only 7 mantissa bits. These 7 mantissa bits equate to 2**23/2**7 = 2**16 times less precision for the bfloat16 format. This means one can generally expect 2**16 consecutive floats expressed in float32 to round to a single bfloat16 expressed float.
Now, for small rational numbers this lack of relative precision does not significantly affect arithmetic for purposes of machine learning as conventional ML training processes are noise resistant. However, for larger scales this poses a significant problem.
Practical Calculations
Indeed, let’s do some calculations to see this. First a bit of context, suppose we want to fine tune a stable diffusion model. Looking at one popular open source model (StabilityAI’s Stable Diffusion 2-1) we see that the median value of the absolute values of its parameters is 0.0129. We will see that the relatively low precision of bfloat16 for floats of this size prevents accumulation of small gradients.
Indeed, consider the following code:
import jax.numpy as jnp
delta = 1e-7
for i in range(10000):
difference = jnp.asarray( 0.0129 ).astype(jnp.bfloat16) - jnp.asarray( 0.0129 + delta*i ).astype(jnp.bfloat16)
if difference > 0:
break
print("Finally noticed a difference at " , delta*i )Finally noticed a difference at 0.0009999Then we see that differences in size of less than 0.0009999 aren’t even registered when added to 0.0129. This means that during training, unless the product of the learning rate and gradient are at least 0.0009999 elementwise, most parameters of the stable diffusion model won’t change at all!
Now to bring this full circle one would need to study the distribution of the elementwise absolute values of the gradients that occur during the process of tuning this stable diffusion model. We don’t have this analysis here, but anecdotally I did notice that stable diffusion models fail to train entirely at low learning rates of 5e-7 but did train successfully to a level matching that of full precision at learning rates of 1.6e-5 (while increasing batch size linearly). Indeed, this observation was the impetus for writing this blog in the first place!
Conclusion
Bfloat16 is far more imprecise than float32, so you may need to use larger batch sizes and learning rates to force training parameters to budge at all during training!
Related Work and Addendum
You might enjoy reading another approach to the problem of bfloat16 precision which uses more complex methods:
Zamirai et al. (2021) “Revisiting BFloat16 Training”. https://arxiv.org/pdf/2010.06192.pdf
You can find a Jax implementation of Zamirai’s stochastic rounding here: https://github.com/nestordemeure/jochastic
As a side note, I’ve noticed that the implementation of stochastic rounding in Nestordemeure’s jochastic repo generates more accurate approximations to the gradient at higher learning rates, so perhaps the strategy of higher learning rates + higher batch sizes in combination with stochastic rounding will yield additive benefits!
If you want to implement jochastic you can modify your TrainState class as follows
import jochasticfrom typing import Any, Callable
from flax import core
from flax import struct
import optaxclass TrainState(struct.PyTreeNode):
"""Simple train state for the common case with a single Optax optimizer.
Synopsis::
state = TrainState.create(
apply_fn=model.apply,
params=variables['params'],
tx=tx)
grad_fn = jax.grad(make_loss_fn(state.apply_fn))
for batch in data:
grads = grad_fn(state.params, batch)
state = state.apply_gradients(grads=grads)
Note that you can easily extend this dataclass by subclassing it for storing
additional data (e.g. additional variable collections).
For more exotic usecases (e.g. multiple optimizers) it's probably best to
fork the class and modify it.
Args:
step: Counter starts at 0 and is incremented by every call to
`.apply_gradients()`.
apply_fn: Usually set to `model.apply()`. Kept in this dataclass for
convenience to have a shorter params list for the `train_step()` function
in your training loop.
params: The parameters to be updated by `tx` and used by `apply_fn`.
tx: An Optax gradient transformation.
opt_state: The state for `tx`.
"""
step: int
apply_fn: Callable = struct.field(pytree_node=False)
params: core.FrozenDict[str, Any] = struct.field(pytree_node=True)
tx: optax.GradientTransformation = struct.field(pytree_node=False)
opt_state: optax.OptState = struct.field(pytree_node=True)
def apply_gradients(self, *, grads, rng,**kwargs):
"""Updates `step`, `params`, `opt_state` and `**kwargs` in return value.
Note that internally this function calls `.tx.update()` followed by a call
to `optax.apply_updates()` to update `params` and `opt_state`.
Args:
grads: Gradients that have the same pytree structure as `.params`.
**kwargs: Additional dataclass attributes that should be `.replace()`-ed.
Returns:
An updated instance of `self` with `step` incremented by one, `params`
and `opt_state` updated by applying `grads`, and additional attributes
replaced as specified by `kwargs`.
"""
updates, new_opt_state = self.tx.update(
grads, self.opt_state, self.params)
new_params = jochastic.tree_add( rng,self.params, updates)
return self.replace(
step=self.step + 1,
params=new_params,
opt_state=new_opt_state,
**kwargs,
)
@classmethod
def create(cls, *, apply_fn, params, tx, rng,**kwargs):
"""Creates a new instance with `step=0` and initialized `opt_state`."""
opt_state = tx.init(params)
return cls(
step=0,
apply_fn=apply_fn,
params=params,
tx=tx,
opt_state=opt_state,
**kwargs,
)